2025年12月23日
2025年12月23日
2025年12月16日
お客様マイページの「連絡ボード」機能を使って、同じ会社のメンバーと簡単にこのページを共有できます。社内で情報を共有し、組織全体の課題解決や業務効率の向上にお役立てください。
- (注)連絡ボードを利用するには企業設定が必要です。
2025年12月23日
2025年12月23日
2025年12月16日
前回の、「7th STEP 第2回:動的公差線図の使い方/全5回」では、真直度に最大実体公差を適用した図面例と、その動的公差線図を確認した。
2017年5月「世界で戦えるGLOBALエンジニアになるための製図技術 7th STEP 第2回:動的公差線図の使い方/全5回」
今回は、姿勢偏差である直角度、位置偏差である同軸度と位置度への最大実体公差を適用した図例と動的 公差線図について説明する。
形状偏差である真直度との違いは、姿勢偏差と位置偏差はデータムを必要とすることである。
データムの有無によって、変化するものがあるかを確認しよう。
段付き軸1をボス2に隙間ばめで挿入する構造を考える。
それぞれのサイズ公差が設定され、挿入部の隙間も小さいことから、穴と軸それぞれに反りやうねりに加えて直角度の傾きが大きいと、互いの基準面(それぞれのデータムA面)を密着させるまで挿入できない恐れがある(図1)。
図1
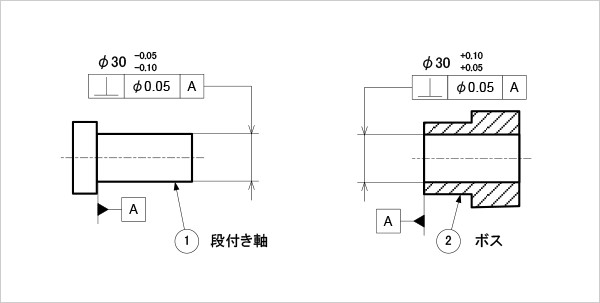
直角度を指示した部品の公差記入例
サイズ公差と直角度の関係のみを動的公差線図に表すと次のようになり、最悪状態でもギリギリ組み立てられることが分かる(図2)。
図2
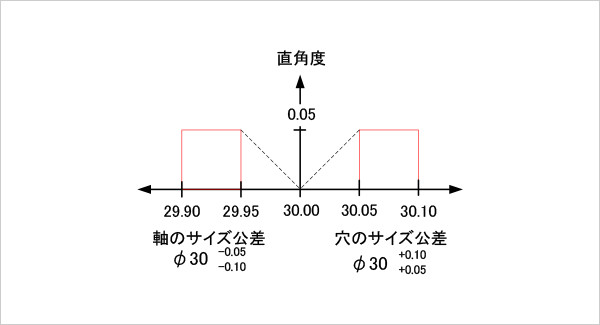
直角度の動的公差線図(サイズ公差と幾何公差の関係のみ)
ここで、最大実体状態でない場合に幾何公差を増やすことができる領域を赤い領域で示すと、次のようになる(図3)。
図3
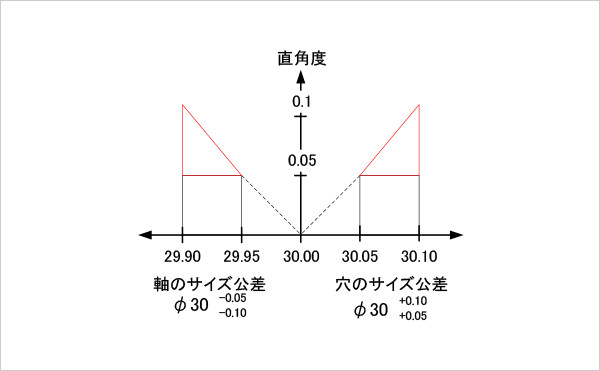
直角度の動的公差線図(最大実体公差方式を適用した場合)
図3の動的公差線図から、最大実体公差を適用した図面例を示す(図4)。
図4
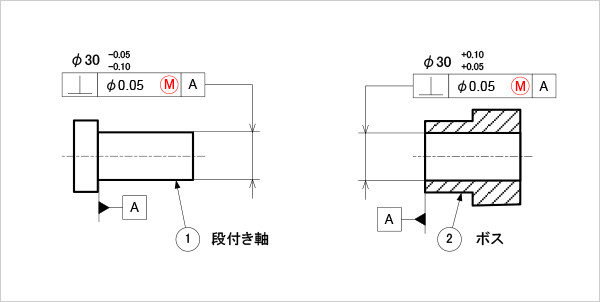
直角度に最大実体公差を適用した部品の図面例
段付き軸1と段付き穴を持つボス2において、それぞれの大径側をデータム基準として、小径側を隙間ばめで挿入する構造を考える。
それぞれのサイズ公差が設定され、大径側と小径側を同時に挿入する必要があるため、それぞれに反りやうねりに加えて同軸度のずれが大きいと、ボスに段付き軸の全てを挿入できない恐れがある。
ここで、それぞれの部品のデータムとなる大径側のサイズには、挿入を保証するために、あらかじめ「包絡の条件![]() (まるイー)」を使って指示している(図5)。
(まるイー)」を使って指示している(図5)。
図5
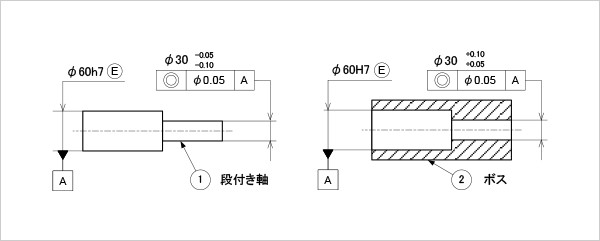
同軸度を指示した部品の公差記入例
幾何特性を与えている該当部のサイズ公差と同軸度の関係のみを動的公差線図に表すと次のようになり、最悪状態でもギリギリ組み立てられることが分かる(図6)。
図6
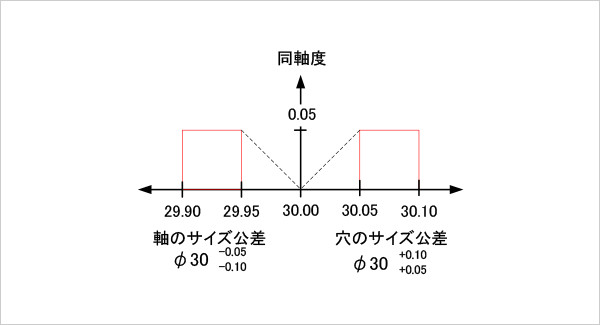
同軸度の動的公差線図(サイズ公差と幾何公差の関係のみ)
ここで、最大実体状態でない場合に幾何公差を増やすことができる領域を赤い領域で示すと、次のようになる(図7)。
図7
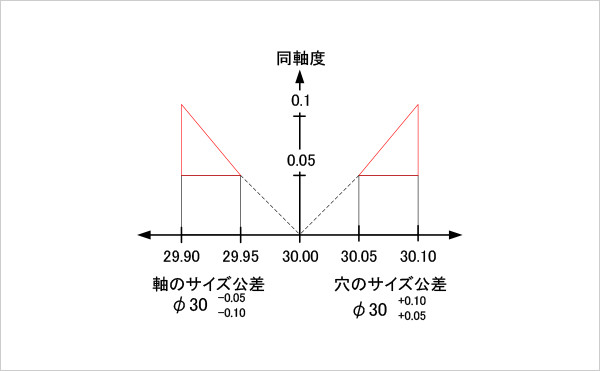
同軸度の動的公差線図(最大実体公差方式を適用した場合)
図7の動的公差線図から、最大実体公差を適用した図面例を示す(図8)。
図8
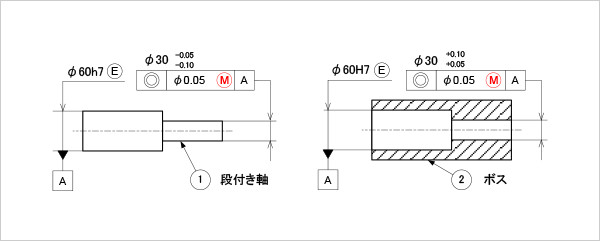
同軸度に最大実体公差を適用した部品の図面例
ブロックピン1とハウジング2において、それぞれの基準である3面を当てながら、軸を穴に隙間ばめで挿入する構造を考える(図9)。
図9
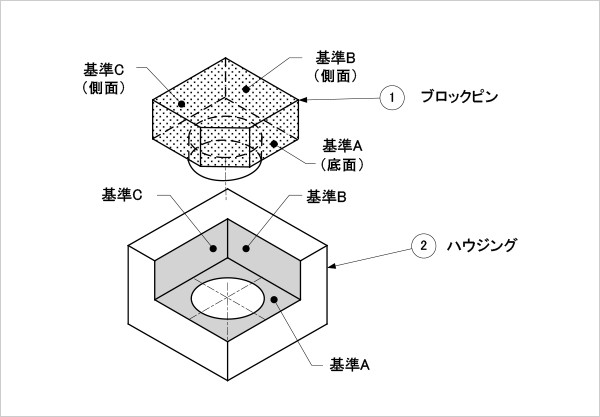
位置度を指示する部品のはめあい構造例
直角度や同軸度と同様に、位置度に最大実体公差を適用した図を示す(図10)。
図10
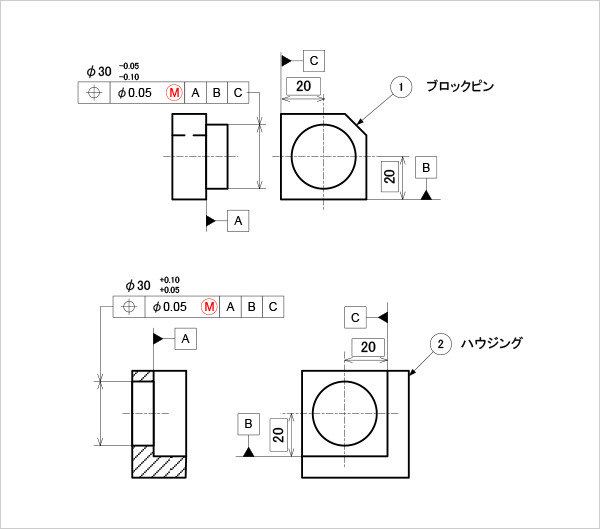
位置度を指示した部品の公差記入例
ここで、最大実体状態でない場合に幾何公差を増やすことができる領域を確認すると次のようになる(図11)。
図11
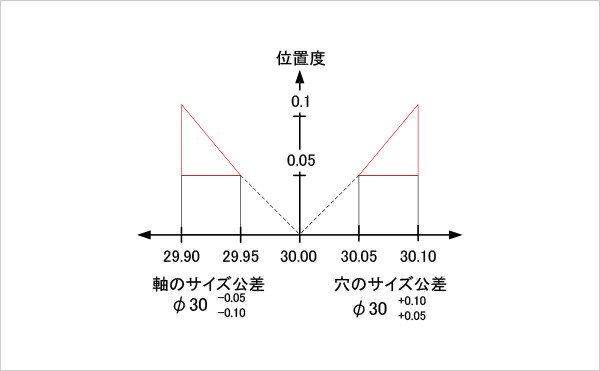
位置度の動的公差線図(最大実体公差方式を適用した場合)
サイズ形体である直角度、同軸度、位置度への最大実体公差を適用した図面例を確認してきた。
ここで、それぞれの動的公差線図を確認すると、直角度、同軸度には一つのデータムが、位置度には三つのデータムが存在しているが、動的公差線図にはデータムとの関係を示した記述がない。
そう、一般的な最大実体公差を指示する場合において、データムの有無は関係ないのである。
ただし、データムがサイズ形体の場合に限り、データムにも最大実体公差を適用することができる。これについては、最終回に説明することにしよう。
偏差の種類やデータムの有無にかかわらず、サイズ形体には最大実体公差方式を適用できることが分かった。
最大実体公差方式を適用していることを示すために、幾何公差値に続けて![]() (まるエム)を記入すればよいことも理解できた。
(まるエム)を記入すればよいことも理解できた。
次回は、最大実体公差を適用した部品を検査するゲージの設計法について解説しよう。
シリーズ記事
2025年12月23日
2025年12月23日
2025年12月16日
お客様マイページの「連絡ボード」機能を使って、同じ会社のメンバーと簡単にこのページを共有できます。社内で情報を共有し、組織全体の課題解決や業務効率の向上にお役立てください。