2025年12月 2日
2025年11月25日
2025年11月25日
お客様マイページの「連絡ボード」機能を使って、同じ会社のメンバーと簡単にこのページを共有できます。社内で情報を共有し、組織全体の課題解決や業務効率の向上にお役立てください。
- (注)連絡ボードを利用するには企業設定が必要です。
2025年12月 2日
2025年11月25日
2025年11月25日
製品設計をする上で、空間認識力が乏しいとスペースを有効に使うことができずに、何度も構想をやり直すことになる。 製品設計の構造段階では、製品の構造として特徴のある面から見た2次元平面上で機能する要素や部品をレイアウトすることから構想が本格的にスタートする。このとき、ベテラン設計者は2次元平面上だけを考えて機能する要素や部品を並べているわけではない。
この時点で、はっきりとしたことは分からずとも、奥行きの空間を見越して要素や部品を平面上にレイアウトしているのである。
0(ゼロ)ステップの目的であるポンチ絵を描くためには、この空間認識力が必要となる。今回は、動作軌跡と奥行きのスペースを意識しよう。
例えば、四節リンクを構想する場合、下図のような二つの構造を考えたとする。 二つの構造を比べると、リンク板の長さと支点間距離が異なる程度の違いしか分からない。
※四節リンクとは、四つの節(ジョイント部)を持ち、そのうち二ヵ所を固定させて一定の動作をさせるリンク機構のことである。
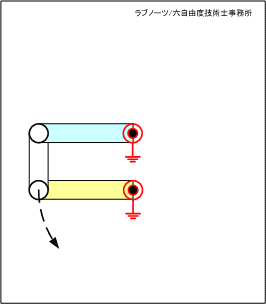
四節リンク構想案(1)
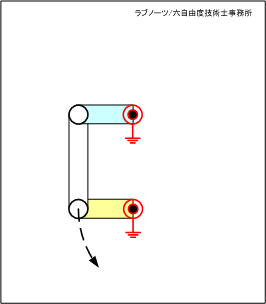
四節リンク構想案(2)
空間認識力は、この静止している構想レイアウト図から二つのポイントを先読みする必要がある。
一つ目は、リンクが動作する軌跡を頭の中で残像として見ることである。
二つ目は、リンクを動作させることを考えたときに、奥行きの構造にどの程度制約が存在するかを推測することである。
一つ目のポイントである動作軌跡は、本来、頭の中でイメージしなければいけないが、説明のためにアニメーションを準備して確認してみよう。
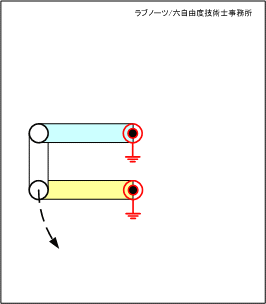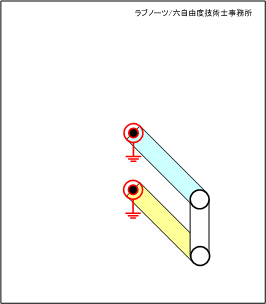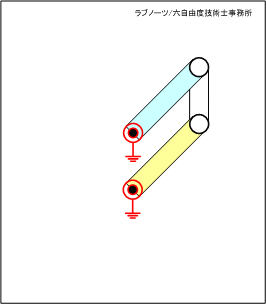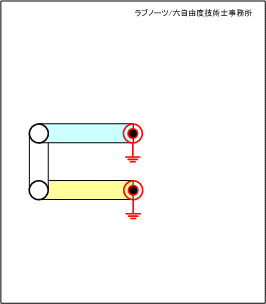
四節リンク構想案(1)
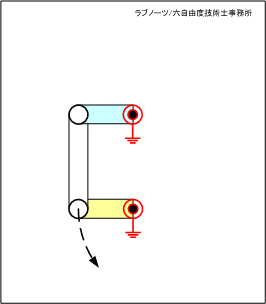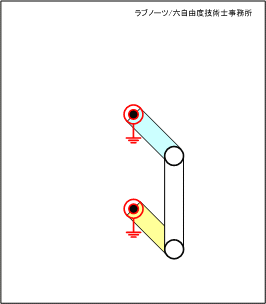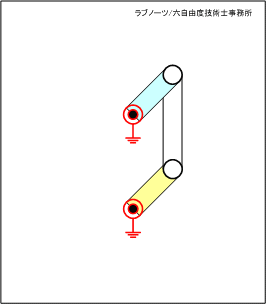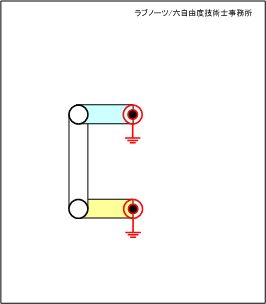
四節リンク構想案(2)
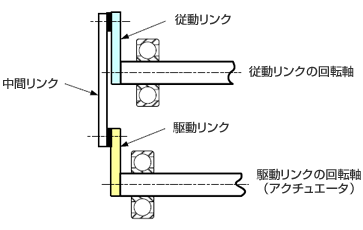
四節リンク構想案(1)は、相対する回転支点をリンク板が横切っていることが分かる。
これに対して、四節リンク構想案(2)は、相対する回転支点をリンク板は横切っておらず、この点が二つの構想案の違いである。
上記の違いを踏まえて、二つ目のポイントである奥行き構造上の制約を推測してみよう。
構想案(1)で、リンク板が回転するには、相手の軸を分断しなければいけなくなる。これを実現するには、二つの回転軸を向かい合わせ、その隙間にリンク板をレイアウトするしか手段がなく、スペース効率や組立性に問題が発生しそうである。
従って、この構造では設計自由度に制約が出ることになり、最悪レイアウトを断念して構想をやり直さなければいけなくなる可能性も大きいといえる。
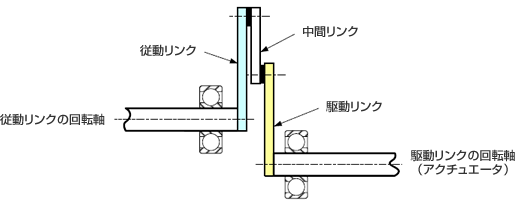
構想案(2)では、リンクを回転させるためには相手の軸を横切る必要がないため、二つの回転軸は同じ方向に向けてレイアウトすることができる。
この構造だと、回転するリンク板は、構造物の端部にレイアウトすることができ、スペース効率や組立性も含めて設計自由度が高い構造であると想像できる。
3次元形状が動作していく過程を頭の中で考え、結果がどのように変化したかという訓練をしてみよう。 下記に示す例題を参考にして、演習問題を解いてみよう。
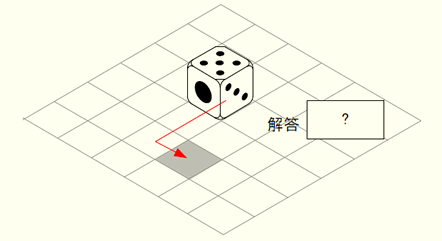
サイコロは床に描いたマス目を移動するたびに転がるという前提で、サイコロを矢印の方向に転がしていったとき、最終地点(灰色のマス目)で上に見える目の数はいくらか?ただし、サイコロの目は表と裏を足すと7になるよう配置されているものとする。
サイコロの目の変化を追いかけていく必要があるが、すべての状態を暗記していくのは大変である。
そこで、図として見える範囲で、最低3 面の目の配置をメモしながら考えるとよい。
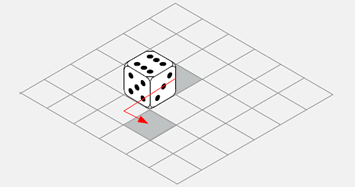
右面が3 のまま、左面に5 が移動、上面に1 の裏にあった6 が出てくる…
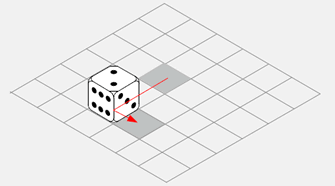
右面が3 のまま、左面に6 が移動、上面に5 の裏にあった2 が出てくる…
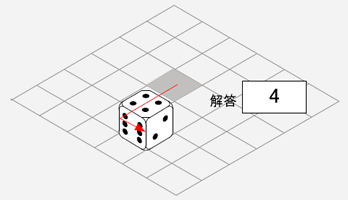
左面が6のまま、右面に2が移動、上面に3の裏にあった4が出てくる… なので、答えは4
サイコロを矢印の方向に転がしていったとき、最終地点で上に見える目の数はいくらか?
ただし、サイコロの目は表と裏を足すと7 になるよう配置されているものとする。
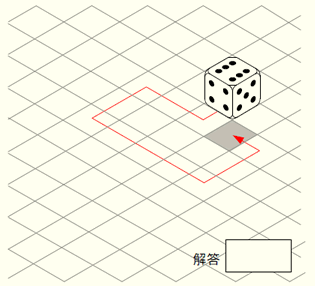

サイコロを準備して転がしていくと、頭を使わずに答えを出すことができる。
しかし、頭の中でサイコロの姿勢が変化していくことをイメージし書きとめながら、立体が空間を移動することを考えるだけでも、空間認識力が鍛えられる。
奥行きをイメージできて初めて、ポンチ絵を描く基本を習得したといえる。
設計センスアップのポイント(2)
次の二つのポイントを抑えることで、設計構想の精度アップを図ることができる。
次回は、足りない投影図から新たな形状を創造し、論理的に考える力を鍛えよう。
シリーズ記事
2025年12月 2日
2025年11月25日
2025年11月25日
お客様マイページの「連絡ボード」機能を使って、同じ会社のメンバーと簡単にこのページを共有できます。社内で情報を共有し、組織全体の課題解決や業務効率の向上にお役立てください。