2025年12月 2日
2025年11月25日
2025年11月25日
お客様マイページの「連絡ボード」機能を使って、同じ会社のメンバーと簡単にこのページを共有できます。社内で情報を共有し、組織全体の課題解決や業務効率の向上にお役立てください。
- (注)連絡ボードを利用するには企業設定が必要です。
2025年12月 2日
2025年11月25日
2025年11月25日
前回までに、寸法公差の記入法や使い方、面の肌記号の意味と記入上の注意点について学習した。
最終回は、寸法公差を図面に記入する際に公差値の妥当性を検証する考え方を解説する。
まずは、一つの部品の中で、寸法配列の違いによって、ばらつきの範囲に影響が出る事例を確認しよう。
例えば、図1左側のように、寸法「50±0.1」と寸法「70±0.2」が直列に並んで指示されている場合、横幅の全長は「120±0.3」となる。
つまり、寸法数値とともに寸法公差も累積して増加することが分かる。
図1
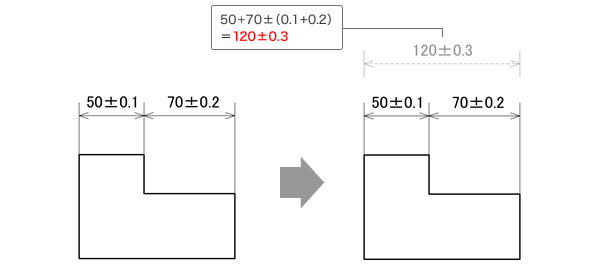
寸法の並列により寸法公差は寸法数値とともに累積して増加する
ここで、「120±0.3」を残して寸法を配列し直した図面を作ってみると、図2の左側のように記入することができる。
この場合に、寸法指示されていない「70」のばらつきを計算してみると、「70±0.4」となり、図1の寸法公差「70±0.2」には戻らないのである。
基準となる寸法数値を引き算する場合、寸法公差だけは累積するため増加するのである。
図2
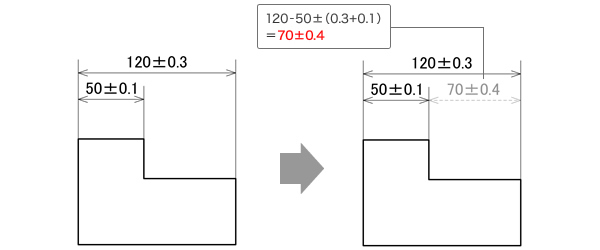
基準となる寸法数値を引き算する場合、寸法公差だけは累積するため増加する
ここで、「70±0.2」に戻らないとおかしいと思う人もいるので、表1で詳しく検証してみよう。
表1
| 項目 | 寸法120±0.3 | 寸法50±0.1 | 計算で求める寸法70 |
|---|---|---|---|
| 最大許容寸法 | 120.3 | 50.1 | - |
| 最小許容寸法 | 119.7 | 49.9 | - |
| 寸法70が最も大きくなる条件 (120が最大、50が最小のとき) | - | 120.3-49.9=70.4 | |
| 寸法70が最も小さくなる条件 (120が最小、50が最大のとき) | - | 119.7-50.1=69.6 | |
| 公差の幅 | 0.6(±0.3) | 0.2(±0.1) | 0.8(±0.4) |
ばらつきの最大最小を具体的な数値で計算してみると、引き算する場合でも、寸法公差は累積するため、足し算しなければいけないことが分かったと思う。
二つの部品を組み合わせる場合のばらつき具合を考えてみよう。
設計者は部品のばらつきを検討する場合、最悪条件に着目して、その組み合わせを検証する。もし、ばらつきによって組み立て不良などが発生すると、設計者の責任として関連部署から叱責(しっせき)の集中砲火を浴びることとなる。
軸と穴を、わずかな隙間を確保しながら手で挿入したいという設計意図がある場合、軸の直径が最も大きい状態で、かつ穴の直径が最も小さい状態のときに、隙間がゼロ以上でないと組むことはできない。
例えば図3に示す条件で、軸を穴に挿入する際の寸法公差の関係を確認してみよう。
図3

図に示した条件で、軸を穴に挿入する際の寸法公差の関係を確認する
公差のばらつき具合を表2で確認してみよう。
表2
| 項目 | 軸(mm) | 穴(mm) |
|---|---|---|
| 基準(ノミナル)寸法 | 50 | |
| 最大許容寸法 | 50.000 | 50.025 |
| 最小許容寸法 | 49.984 | 50.000 |
| 寸法公差(公差の幅) | 0.016 | 0.025 |
| はめあいの種類 | すきまばめ | |
| 最小すきま | 0.000 | |
| 最大すきま | 0.041 | |
従って、軸は最大寸法50.0から必ず小さくなる方向にばらつき、穴は最小寸法50.0から必ず大きくなる方向にばらつくことから、必ず隙間ゼロ以上を確保していることが分かる。
ここで、気になる点が一つある。寸法のばらつき具合によっては、隙間がゼロになる組み合わせが存在することである。
寸法公差のばらつき範囲の中で、限界値ぎりぎりの寸法で出来上がる確率はどのくらいであろうか?
一般的に、加工者は寸法公差の中央値を狙って加工するが、加工機械の精度、取り付け時の位置ずれ、工具の摩耗などによって、プラス側かマイナス側にばらつきが発生してしまう。
大量生産する部品において、全数検査をすることは不可能である。そこで、ロットごとに抜き取り検査をすることで、検査しなかった部品まで合格として判断する。
その根拠となるものが、統計学で用いられる正規分布である。
正規分布を図4に示す。
正規分布とは、平均値の付近に集積するデータの分布を表した連続的な変数に関する確率分布で、左右対称の山形で表現される。
つまり、正規分布に従い、寸法公差の中央値に近い部品の数が多く寸法公差の限界値に近い部品がかなり少ない状況に工程を管理することができれば、抜き取り検査が可能となる。
図4
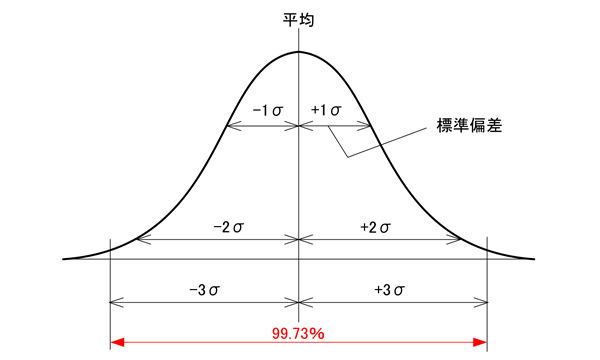
抜き取り検査で合格とするための根拠となる正規分布図
寸法のばらつきが正規分布し、より小さな標準偏差を持つように工程設計を行う部門が生産技術の役割でもある。
この統計学にある正規分布の考え方を使った公差の検討を、「分散の加法性を使った公差検討」と言う。
具体的な事例を使って、統計的な公差解析の計算方法を確認しよう。
図5のように、ハウジングの中にA~Dの四つの部品を挿入する場合の、ハウジングの寸法設定を考えてみよう。
しかし、できる限り四つの部品とハウジングの隙間は最小にしたいという設計意図があるとする。
図5
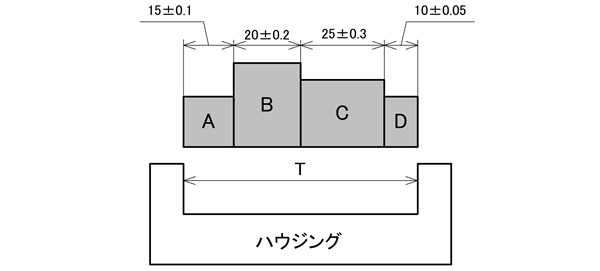
四つの部品の寸法とハウジングの関係
まずは、図面上の公差の累積を計算する手法である「算術的な公差検討」で計算してみよう。
算術的な公差検討では、ハウジングの寸法Tは、次式で計算する。
![]()
![]()
この計算では、ハウジングの寸法Tは、70.65mm以上にしなければ、4つの部品を挿入することはできない。
次に、部品のばらつきが正規分布であることを前提とした「統計的な公差検討」で計算してみよう。
統計的な公差検討では、ハウジングの寸法Tは、次式で計算する。
![]()
![]()
この計算では、ハウジングの寸法Tは、70.38mm以上でよいことになる。
このように、統計的な公差解析を使うと、四つの部品の寸法公差を変えることなく、考え方を変えるだけで、累積する公差を小さくできるというメリットがある。
特に大量生産の製品は、この考えが存在するからこそ成り立っているといっても過言ではない。
統計的な公差解析を使う際の注意点として、次の2点がある。
機能や組み立てを保証する設計意図を明確に第三者に伝えるためには、寸法公差は必要不可欠な要素であることが理解できたと思う。
寸法公差は、記入するだけでなく、その正当性を検証する作業も同時に行わなければいけないことも理解できたと思う。
以上で、「世界で戦えるGLOBALエンジニアになるための製図技術 4th STEP <全5回>」を完結する。
しかし、グローバルな視点で図面を見ると、まだ完成というわけにはいかない。
機能上の要求に加えて、加工によって形が崩れることを制御する必要がある。特に海外で問題になるのは、このカタチの崩れである。
これらは、次の機会にお話しすることとしよう。
シリーズ記事
2025年12月 2日
2025年11月25日
2025年11月25日
お客様マイページの「連絡ボード」機能を使って、同じ会社のメンバーと簡単にこのページを共有できます。社内で情報を共有し、組織全体の課題解決や業務効率の向上にお役立てください。