2025年12月 2日
2025年11月25日
2025年11月25日
お客様マイページの「連絡ボード」機能を使って、同じ会社のメンバーと簡単にこのページを共有できます。社内で情報を共有し、組織全体の課題解決や業務効率の向上にお役立てください。
- (注)連絡ボードを利用するには企業設定が必要です。
2025年12月 2日
2025年11月25日
2025年11月25日
前回は、加工によってカタチが崩れる理屈を理解した。
設計者として幾何公差を図面に記入する際に気になるのが、「この幾何公差って、どうやって測定すればいいの?」っていう問い合わせである。
その際に、「いやー、ちょっと分かりません…」とは言いづらいものである。そこで、設計者として方向性だけでも回答できるよう、第3回では知っておきたい計測機器の基礎知識を解説する。
第1回の「独立の原則」で説明したように、寸法は2点間の直線距離を測定するものであり、幾何特性を計測することができない。そのため、幾何公差を測定する際には、寸法を計測するためのツールであるノギスやマイクロメータを使うことができない。
表1に示すように、幾何特性は定盤やブロックゲージを基準として使用しながら、ダイヤルゲージや三次元測定機を使って計測する。専用機である真円度測定機も複数の幾何特性を測定できることが特徴である。
表1 製図と計測の関係
| 大きさ・長さ | 幾何特性(カタチ) | 表面の粗さ | |
|---|---|---|---|
| 図面指示 | 寸法(公差)数値 | 幾何公差値 | 表面性状の図示記号 |
| 定義 | 形体の実寸法(2点測定による)だけを規制する。 | 形体の寸法に無関係に、その形体の理論的に正確な形状または姿勢または位置からの偏差を規制する。 | 対象物の表面、除去加工の要否および表面粗さについて行う。 |
| 代表的な計測器 | ノギス マイクロメータ シリンダゲージ プラグ/リングゲージなど | 定盤、ブロックゲージ ダイヤルゲージ 真円度測定機 三次元測定機など | 表面粗さ測定機 |
さて、皆さんは測定環境の室温は何度が妥当か知っているだろうか?
地球上の物質は必ず、温度が上がると膨張し、温度が下がると収縮する。従って、温度によって寸法や形状は変化してしまうのである。
世界的に測定環境の温度は20℃と決められている。
つまり幾何公差を測定する際は、夏でもエアコンがガンガン掛かった肌寒いくらいの部屋で測定されるものと覚えておこう。
それでは、代表的な計測器の特徴をみていこう。
・・・形状測定の基準となるもの(図1)
定盤には石製の定盤(磁石が付かない)と鋳鉄製の定盤(磁石が付く)の2種類がある。
図1

左:石製の定盤、右:鋳鉄製の定盤
計測の基準となる定盤といえども、残念ながら平面度ゼロに仕上げることは不可能である。JISでは、表2のように、等級ごとに平面度を規定している。
表2 250×250mmの部分面積における定盤の平面度
| 等級 | 0 | 1 | 2 |
|---|---|---|---|
| 平面度(μm) | 3.5 | 7 | 15 |
・・・平行や高さの基準となるもの(図2)
ブロックゲージは、高い精度の平面度と平行度を持ち、かつ2面間の寸法精度を保つよう仕上げられた直方体で、セラミックスなど硬くて磨耗しにくく、熱膨張の影響の少ない材料によって製作される。
図2

ブロックゲージ
・・・平行や高さを比較測定するもの(図3)
ダイヤルゲージはハイトゲージ台の先端に取り付け、ブロックゲージなどを基準として、それとの差を比較計測したり、平行度や直角度、回転振れなどを確認したりするのに使用する。
図3

ダイヤルゲージ
・・・真直度、真円度、円筒度、平行度、直角度、同軸度、円周振れ、全振れを測定するもの(図4)
真円度測定機は、回転テーブルを持ったものが一般的で、スタイラス(接触子)を測定対象部品に接触させることでさまざまな幾何特性を測定するものである。
図4

真円度測定機
・・・自由曲面を含め、全ての幾何特性を測定するもの(図5)
接触式の三次元測定機は、熱膨張の影響の少ないルビーやセラミックス製で球体のスタイラス(図6)を持ち、測定対象物を点、あるいは線として測定をし、三次元上の座標値を検出する(図7)。
図5

接触式三次元測定機
図6

スタイラス
図7

測定の様子
接触式三次元測定機のスタイラスが接触した座標から形状を演算する。
表3 接触式三次元測定機の原理
直線 円筒面や平面の表面上の最低2点を触ることで直線を定義する
| 平面 平面上の最低3点を触ることで平面を定義する
| 円の外形 円筒面上の最低3点を触ることで円を定義する
|
楕円の外形 楕円筒面上の最低4点を触ることで楕円を定義する
| 円の中心点 円筒面上の最低3点を触ることで円の中心点を演算する
| 円筒の中心線 円筒面上の最低3点かつ2カ所を触ることで円筒の中心線を演算する
|
自由曲線 自由曲面上の直線状の複数点を触ることで自由曲線を定義する
| ||
自由曲面 自由曲面上の全面にわたり、複数点を触ることで自由曲面を定義する
| ||
表3では、測定するための最低必要点数を列記したが、それ以上の点を測定する場合、それら全ての点を通過する形状は、真の形状からカタチが崩れてしまう(図8-a)。
このような場合、一般的に「最小二乗法」を使用する。
円を例にすると、各測定点の径方向の偏差の二乗和が最小となる平均円を求める方法である(図8-b)。
図8
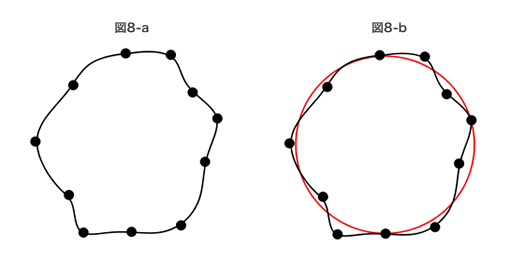
最小二乗法の考え方
計測方法の原理をイメージできるだけでも、正しく幾何公差を使いこなすことができると確信する。
幾何公差を使ううえでみそになるのがデータムである。多くの設計者が正しいデータムの記入法を理解せずに図面を描いている。次回は正しいデータムの使い方と記入法を解説するとしよう。
シリーズ記事
2025年12月 2日
2025年11月25日
2025年11月25日
お客様マイページの「連絡ボード」機能を使って、同じ会社のメンバーと簡単にこのページを共有できます。社内で情報を共有し、組織全体の課題解決や業務効率の向上にお役立てください。