シリーズ記事
4 位置偏差の使い方
前回は、姿勢偏差の「平行度」と「直角度」、「傾斜度」について学んだ。
今回は、位置偏差に分類される「同軸度/同心度」と「対称度」、「位置度」について説明する。
位置偏差
位置偏差とは、「対象となる形体が、データムに関連して中心点や、中心線、中心平面、形状などが幾何学的に正しい位置に存在するかを表す偏差の許容値内にあるかを規定する」と定義される。
姿勢偏差と同様に、データムを参照することが特徴である。ただし、位置度についてはデータムを用いずに指示することもできる。
位置偏差には、次の五つの幾何特性がある。
- 同軸度／同心度
- 対称度
- 位置度
- 線の輪郭度
- 面の輪郭度
今回、「線の輪郭度」と「面の輪郭度」の説明は割愛する。
1-1. 同軸度
同軸度とは、「データム軸直線と同一直線状にあるべき中心軸のデータム軸直線からのひらきの許容値」と定義される。
つまり、同軸度の評価対象となる形体は、「データム中心線に対して同一直線上の位置に設計された中心線」と認識すればよい。
同軸度が適用する公差領域は、次の1種類のみである。
- データム中心線に対して同一直線上に中心線を持つ円筒の領域（3次元空間）
1-2. 同心度
同心度とは、「データム円の中心に対する他の円形形体の中心の位置のひらきの許容値」と定義される。
つまり、同心度の評価対象となる形体は、「データム中心点に対して同一平面上の位置に設計された中心点」と認識すればよい。
同心度が適用する公差領域は、次の1種類のみである。
- データム中心点に対して同一平面上に中心線を持つ円の領域（2次元平面）
同軸度と同心度の違いは、奥行きの長さ（軸線の長さ）で使い分ければよい。ただし、明確に使い分けるための数値は決まっていないため、感覚的に軸線が短いもの（ワッシャーのような薄い板金部品）は同心度と呼び、軸線にある程度長さのあるもの（段付き軸など）は同軸度と呼ぶとよい。
1） 同軸度の指示
図1
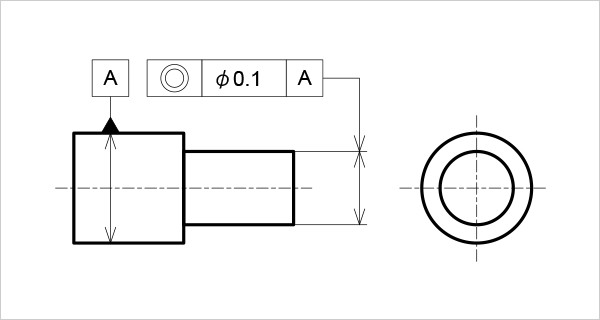
同軸度の指示例
公差領域は、赤い領域になる（図2）。
図2
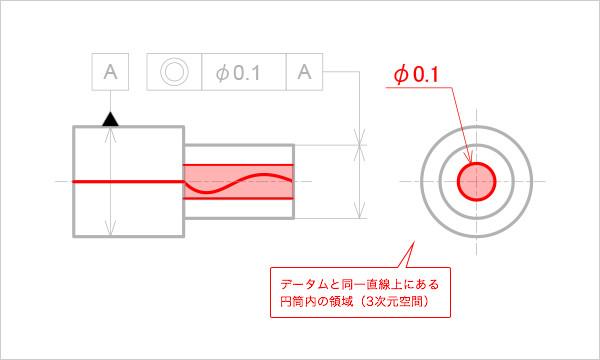
同軸度の公差領域
2） 同心度の指示
同心に設計された薄板に同心度を指示する場合、データム記号をデータム側の直径の寸法線に一致させ、かつ指示線の矢を対象となる寸法線に当て、幾何公差値に必ずφを付ける（図3）。
図3
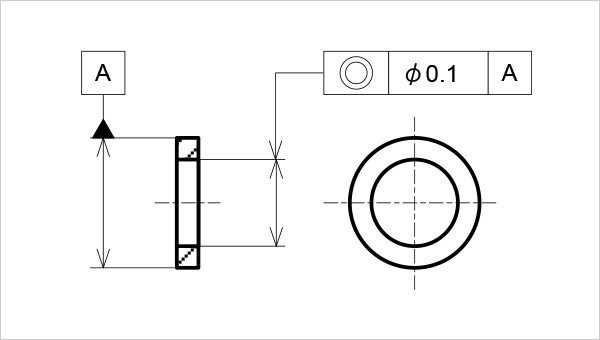
同心度の指示例
公差領域は、赤い領域になる（図4）。
図4
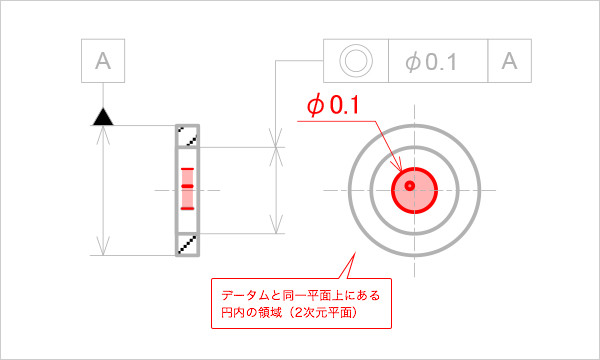
同心度の公差領域
真円度測定機を使った場合の同軸度計測イメージを写真1に示す。
データム円筒面上の任意の円周を2カ所以上測定することでその中心軸をデータムとして設定し、対象となる円筒面上の任意の円周を2箇所以上測定することで対象となる中心線を導き評価する。
※本例は一例であり、他の計測方法も存在する。
写真1
同軸度の計測イメージ
ここで、同軸度の公差領域をもう一度確認してみよう。
データム中心軸と同一線上に中心線を持つ円筒が公差領域であるが、前回に説明した平行度との関係はどう考えればよいのだろうか？
そう、同軸度を満足するためには、自動的に平行度や真直度も満足しなければならない。
つまり、今回の位置偏差である同軸度は、前回と前々回に説明した姿勢偏差である平行度と形状偏差である真直度も含むと考えればよい（図5）。
図5
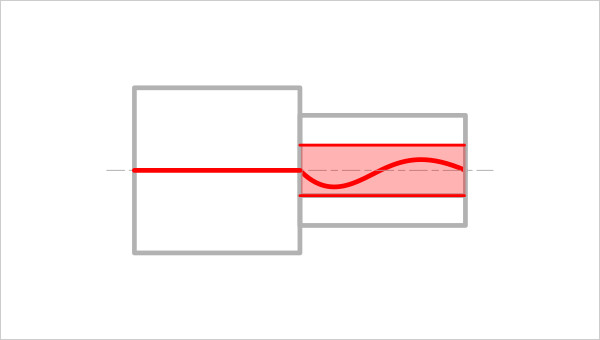
真直度と平行度を含む同軸度の公差領域
2. 対称度
対称度とは、「データム軸直線またはデータム中心平面に対して対称であるべき形体の対称位置からのひらきの許容値」と定義される。
つまり、対称度の評価対象となる形体は、「データム中心平面に対して同一平面上の位置に設計された1枚の中心平面または1本の中心線」と認識すればよい。
対称度が適用する公差領域は、次の1種類のみである。
- データム中心平面に対して同一平面上に中心平面を持つ平行2平面間の領域（3次元空間）
1） 中心平面同士の対称度
ブロックの中央に配置した溝に対称度を指示する場合、データム記号をデータム側の寸法線に一致させ、かつ指示線の矢を対象となる溝の寸法線に当て、幾何公差値にφは付けない（図6）。
図6
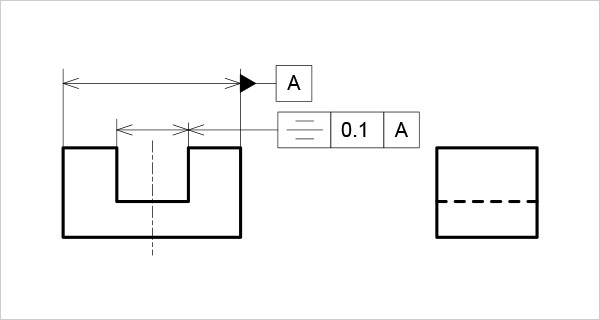
対称度の指示例（中心平面同士）
公差領域は、赤い領域になる（図7）。
図7
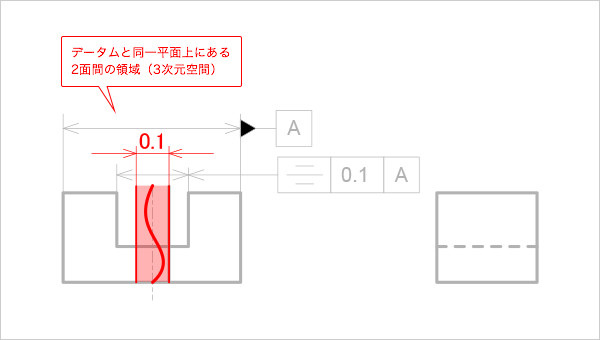
対称度の公差領域（中心平面同士）
2） 中心線同士の対称度
円筒軸の中央に配置した穴に対称度を指示する場合、データム記号をデータム側の寸法線に一致させ、かつ指示線の矢を対象となる穴の寸法線に当て、幾何公差値にφは付けない（図8）。
図8
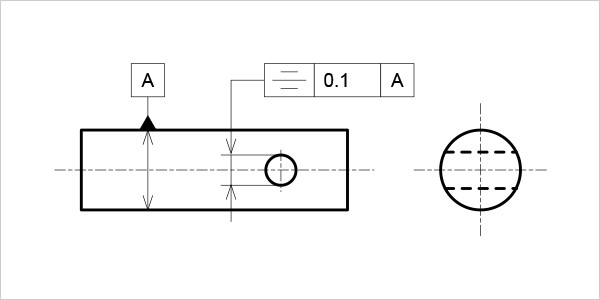
対称度の指示例（中心線同士）
公差領域は、赤い領域になる（図9）。
図9
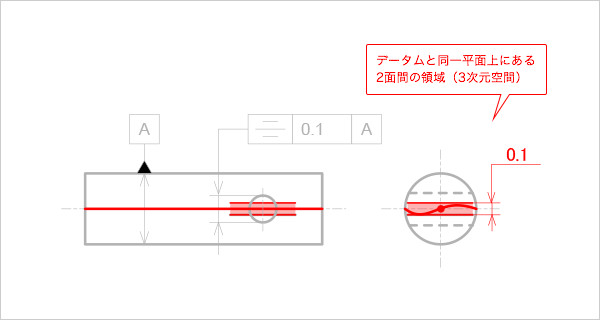
対称度の公差領域（中心線同士）
3次元測定機を使った場合の対称度計測イメージを写真2に示す。
ブロックの両側面を触ることで中心平面をデータムAとして設定し、溝の内側の2面を触ることで、対象となる溝の中心平面の位置を評価する。
※本例は一例であり、他の計測方法も存在する。
写真2
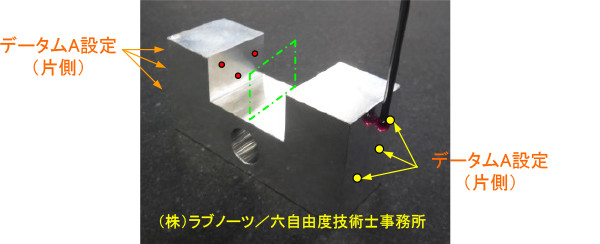
対称度の計測イメージ
3. 位置度
位置度とは、「データムまたは他の形体に関連して、定められた理論的に正確な位置からの点、直線形体、または平面形体のひらきの許容値」と定義される。
つまり、位置度の評価対象となる形体は、「データムに対して理論的に正確な位置にある形体」と認識すればよい。
位置度が適用する公差領域は、次の5種類である。
- データムに対して理論的に正確な位置にある2枚の平面間の領域（3次元空間）
- データムに対して理論的に正確な位置にある2本の直線間の領域（2次元空間）
- データムに対して理論的に正確な位置にある円柱の領域（3次元空間）
- データムに対して理論的に正確な位置にある円の領域（2次元空間）
- データムに対して理論的に正確な位置にある球の領域（3次元空間）
・穴の位置度
ある位置に設計された複数の穴に位置度を指示する場合、データム面から理論的に正しい位置を表す理論寸法と共に、穴の寸法線を表す引き出し線に幾何公差をつける（図10）。
本例では公差領域を円柱領域で設定したため、幾何公差値にφを付けている。
図10
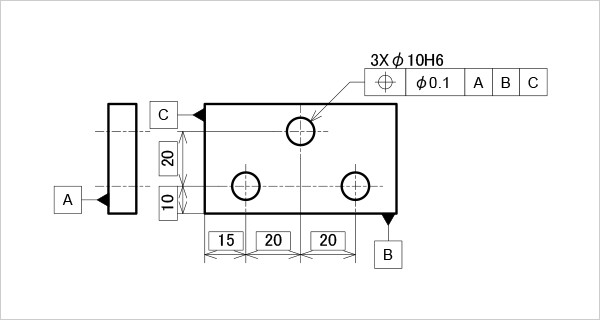
位置度の指示例
公差領域は、赤い領域になる（図11）。
図11
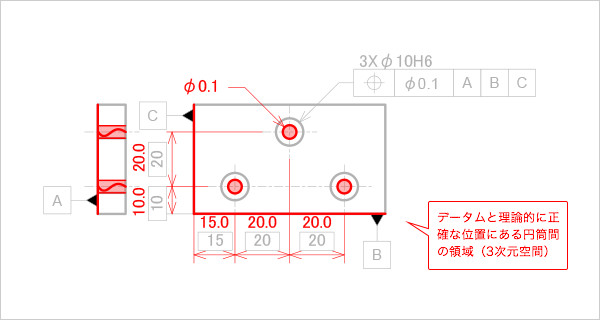
位置度の公差領域
図5で説明したように、位置偏差は姿勢偏差や形状偏差を含むため、図11のデータムAの役割は公差領域となる円筒がデータムAに対して直角になることを示している。
3次元測定機を使った場合の位置度計測イメージを写真3に示す。
実用データムである定盤にデータムA面を当て、定盤を触ることでデータムAとして設定し、二つの側面を触ることで、それぞれデータムB、データムCと設定する。対象となる穴の円筒面を測定することで中心軸の位置を評価する。
※本例は一例であり、他の計測方法も存在する。
写真3
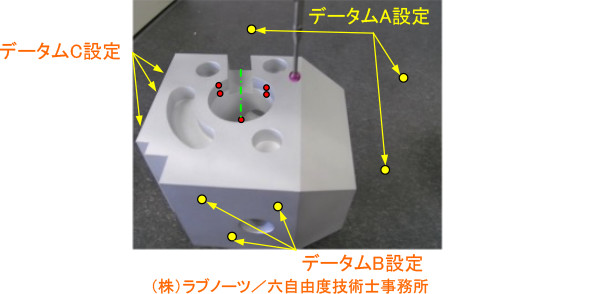
位置度の計測イメージ
位置偏差は、比較対象となるデータムが必要である。
（位置度に関してはデータムがなくても使える場合がある）
位置偏差は姿勢偏差を含んでおり、自動的に形状偏差も含むことが分かった。
位置偏差と姿勢偏差の違いは、公差領域があるべき位置に固定されることである。
最終回となる次回は、振れ偏差の二つの特性（円周振れ、全振れ）と、偏差の相関関係のまとめを解説しよう。
シリーズ記事