この連載について
前回は、最大実体公差を検査する機能ゲージについて学習した。今回は、幾何公差の値にゼロを記入する「ゼロ幾何公差方式」と、データムに最大実体公差を適用する「データムの浮動」について説明する。
【お知らせ】がんばる企業応援マガジン最新記事のご紹介
1 ゼロ幾何公差方式
前回までの解説によって、最大実体公差とは、サイズのばらつき具合によって、組み立てにマージンがあるときに限り幾何公差を広げることができ、不良率が下がることで部品のコストダウンにつなげるテクニックであることを理解した。
実は、さらにコストダウンを図ることができる「ゼロ幾何公差方式」が存在する。
しかし、幾何公差の数値をゼロにするだけでは、「一切の幾何偏差の崩れを許さない」という意味になり、加工するうえで現実的ではない。
そこで、幾何公差値のゼロに続けて○Mを記入することで、最大実体状態のときに限り幾何偏差ゼロを要求し、最大実体状態でないときにはその差分に応じて幾何偏差の崩れを許すものがゼロ幾何公差方式である(図1)。
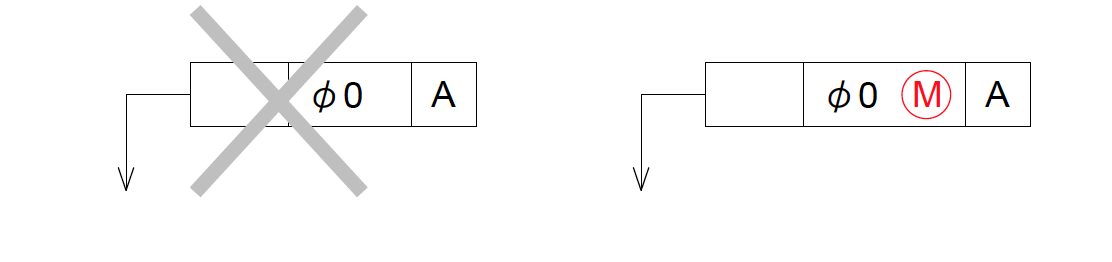
図1:ゼロ幾何公差方式の指示例
最大実体公差を同軸度に適用した図面を、ゼロ幾何公差方式に変更してみよう(図2)。
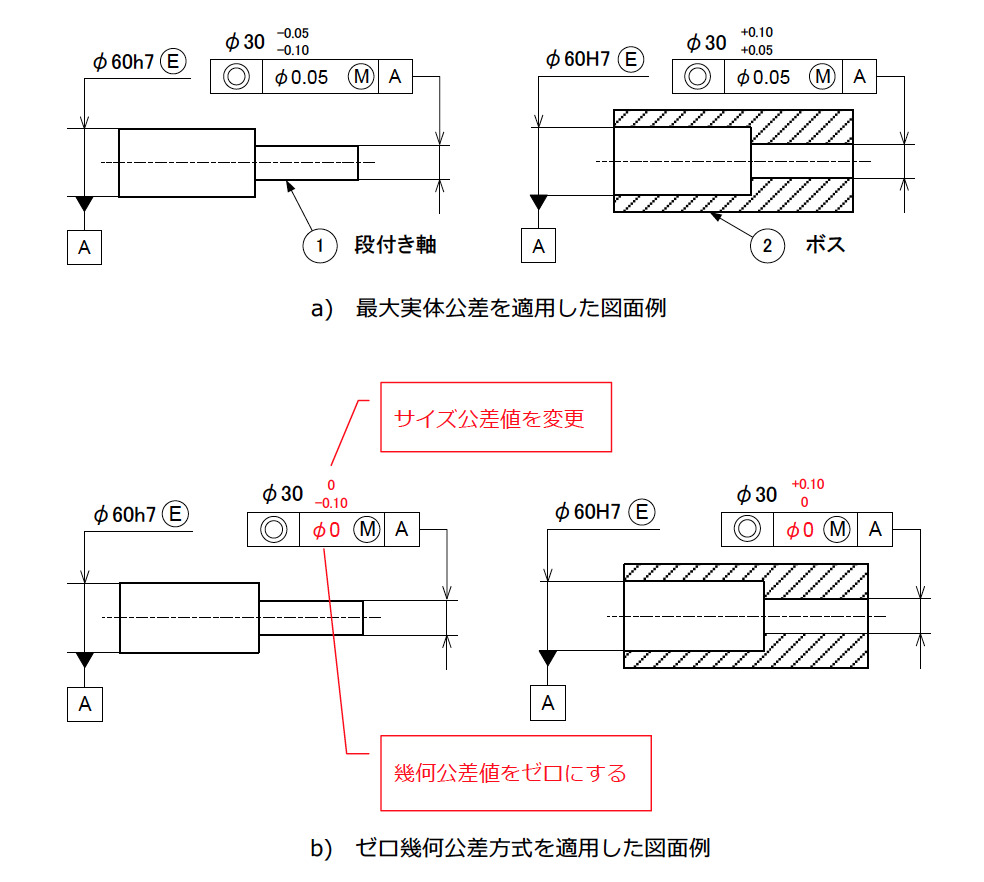
図2:同軸度の図面例
図2 b)を見ればわかるように、ゼロ幾何公差方式を適用する場合、幾何公差値をゼロにするだけではいけない。合わせてサイズ公差値も変更する必要がある。
サイズ公差値の変更については、動的公差線図を見れば理解できると思われる。
ゼロ幾何公差方式によって増やしたサイズ公差の領域を示すと、次の赤い領域になる(図3)。
つまり、幾何公差は厳しくする代わりに、サイズ公差の範囲を広げるものである。
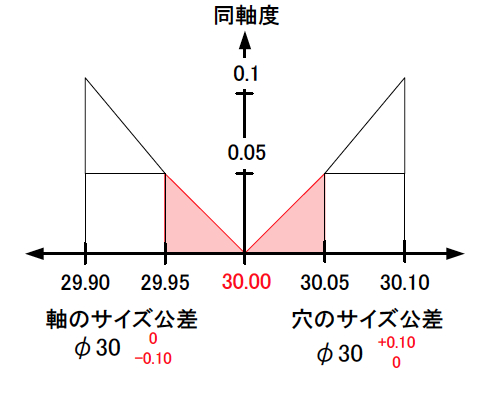
図3:ゼロ幾何公差方式を適用した同軸度の動的公差線図
同様に、最大実体公差を位置度に適用した図面をゼロ幾何公差方式変更にしてみよう(図4)。
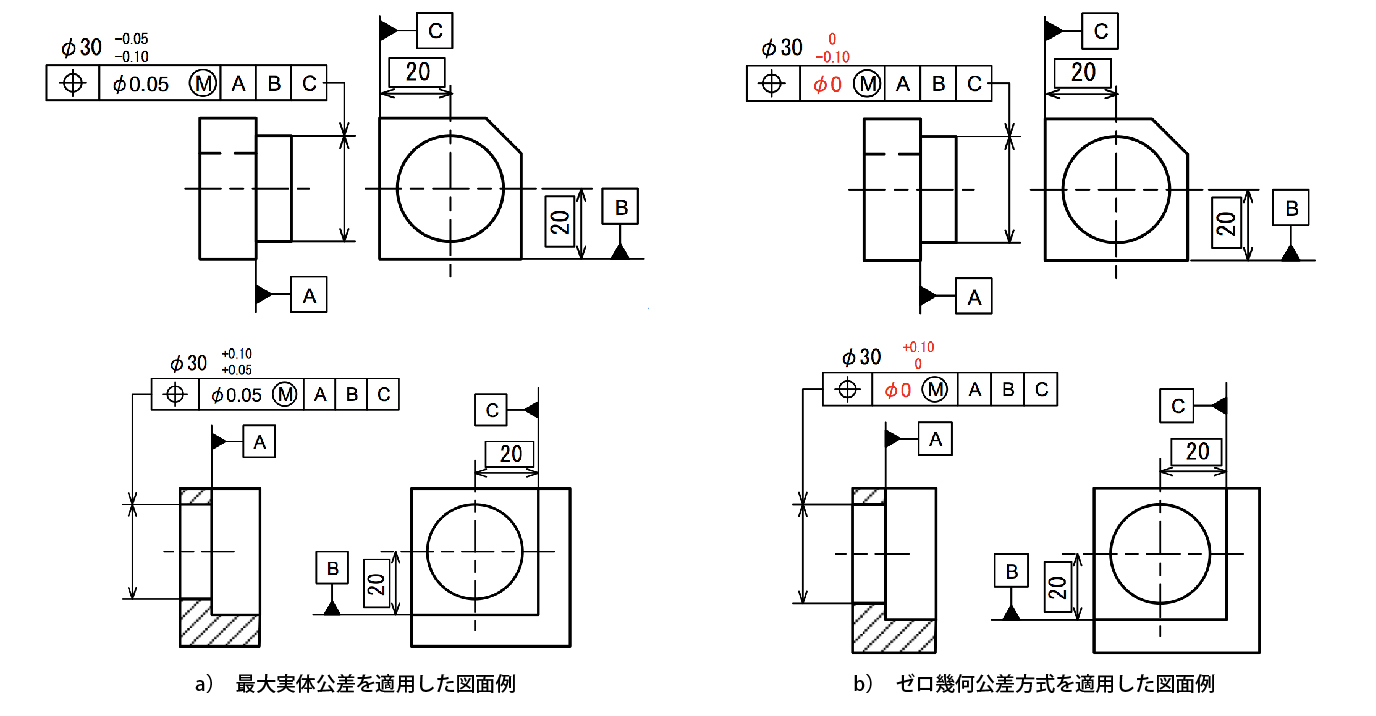
図4:位置度の図面例
ゼロ幾何公差方式によって増やしたサイズ公差の領域を示すと、次の赤い領域になる(図5)。
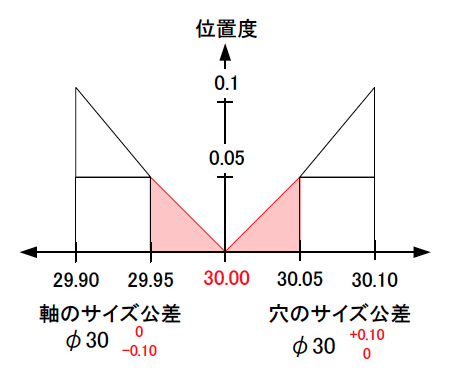
図5:ゼロ幾何公差方式を適用した位置度の動的公差線図
以上のことから、同軸度でも位置度でも考え方や図面指示に違いがないことが分かったことと思う。
2部品のサイズ公差を図示サイズ(基準となるサイズ)から始まるように設定し直したうえで、幾何公差値のゼロに続けて○Mを記入すればよいのである。
ゼロ幾何公差方式は、おおげさで使いづらいと思うかもしれない。
しかし、真直度の例を挙げると、ゼロ幾何公差方式は「包絡の条件」と全く同じ意味となることが分かり、特に難しいテクニックではないということを認識しよう(図6)。
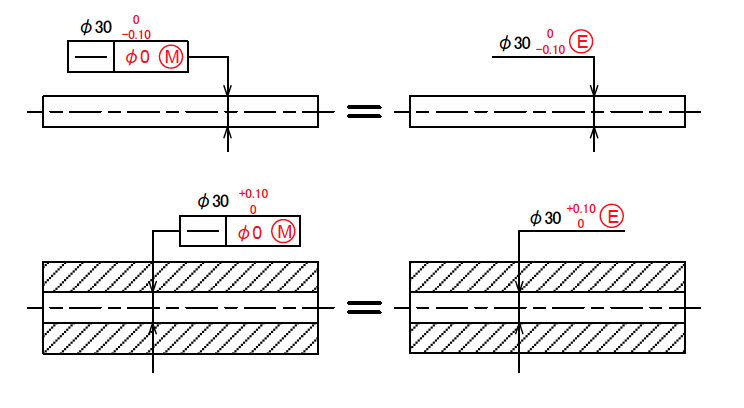
図6:ゼロ幾何公差方式と包絡の条件の関係(真直度の例)